Water-Soluble Drag Reducing Polymers within the context of Hydraulic Fracturing
Polyacrylamide HPAM HVFR Friction Reducers Reynolds Number Friction Factor Polymer Degredation Molecular Weight
Introduction
Hydraulic Fracturing technology was first introduced to the oil and gas industry in 1949 in the United States with Halliburton's patented "hydrofrac process"(Pardo & Torres-Verdin, 2012). Since its inception, hydraulic fracturing has been based on the same fundamental principles. Inject fluid at sufficiently high pressure down a wellbore into a low-permeability hydrocarbon-bearing reservoir to fracture the subsurface rock, inject a solid propping agent to keep induced fractures open once the pressure is released, and ensure the propping agent provides a conductive channel to flow hydrocarbons out of the reservoir once complete. Hydraulic fracturing substantially improves the recovery and production of both liquid and gas hydrocarbons providing an economically beneficial extraction process. Though basic in theory the formulation of the hydraulic fracturing fluid utilized within the industry has continually developed to address multiple reservoir, operational, and economic challenges.
Over the past 10 years, a surge in the consumption of water-soluble friction reducers has offered oil and gas operators an efficient, low-cost means of performing hydraulic fracturing treatments. These types of treatments are commonly referred to as "slickwater" operations where the fluid formulation consists of 1-5 gallons of friction reducer per thousand gallons of freshwater injected at a high rate to carry sand deep into the reservoir to generate conductive fractures. This work intends to review the body of research and present the current understanding of drag-reducing water-soluble polymers as offered through scientific journals and academia, and associate it's implication within the context of the hydraulic fracturing industry to provide a greater understanding and ideas on improving overall performance and efficiency for future operations.
Friction Reducers
When long-chain polymers are introduced in dilute concentrations into turbulent pipe flow evolves a phenomenon that significantly reduces the amount of fluid friction, or energy loss, experienced across a pipe length as first described by Toms in 1948(Toms, 1948). Friction reducers substantially reduced the amount of energy required to pump and flow fluids through tubulars. This technique is commonly referred to as drag reduction by polymer additives and has been extensively studied over the past 80 years. Friction reduction by polymer additives has been widely applied across multiple industries as it provides attractive economic advantages in practice by allowing either a substantial increase in fluid flow rate or by providing a significant reduction of pressure within hydraulic systems where throughput cannot be solved by additional or larger volume flowlines. One of the earliest and most notable applications of drag reduction by polymer additives was their use in the Trans-Atlantic pipeline allowing for less demanding pumping equipment requirements and greater throughput of hydrocarbon transport(Burger, Munk, & Wahl, 1982). Drag reducers continue to be used in pipelines today as well as across city sewage, drainage infrastructure, circulatory medicine, firefighting, oil and gas production, agriculture, and various mechanical and lubricated components(Morgan, 1990).
Chemical Composition
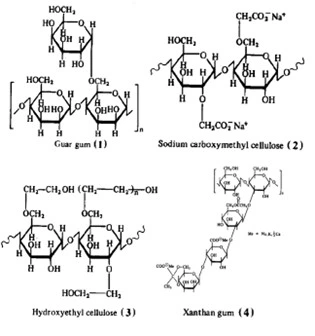
Several water-soluble drag-reducing polymers are naturally occurring (Wever, 2011). Studies have illustrated aquatic species have mucous secretions to minimize drag in their natural habitats for intermittent bursts of speed. Other polysaccharides exist in nature and are produced by plants, animals, and microbes to various degrees. Guar gum and cellulose are two of the most widely used naturally occurring polysaccharides that have been applied throughout the oil and gas industry due to their drag-reducing and viscosity building potential. These polymers contain semi-rigid backbones due to large cyclohexane constituents and demonstrate strong shear-resistance beneficial to high-flow applications. Functionalized variants of both guar and cellulose include hydroxyl-ethyl and carboxy-ethyl side chains to allow for an additional charge and bonding characteristics to crosslink polymer stands and produce a stout gel with salinity and variable pH compatibility. Another commercially used bacteria-produced polymer is xanthan gum comprised of a rigid backbone and flexible, charged sidechains. The large sidechains limit flexibility and add to the rigidity allowing for shear stress resistance in fluid flows which exceed that of cellulose or guar gum (Morgan, 1990). These polymers all form high molecular weight linear chains whereas polymers that generate highly branched structures have been shown to have poor drag-reducing characteristics. The main drawback of naturally occurring biopolymers is their susceptibility to biodegradation by microorganisms which can manifest problematic side effects. Specific applications conducted in the presence of sulfate-reducing bacteria can evolve toxic H2S. The molecular structure of the most common naturally produced drag-reducing polymers are illustrated in Figure 1.
Figure 1: Chemical composition of naturally occurring water soluble drag reducing polymers (Morgan, 1990).
Many drag-reducing agents used in modern applications are synthetic polymers that reduce drag in substantially smaller and more economic concentrations suitable for large scale use. Polyethylene oxide (PEO) is a long chain, flexible polymer, and has been extensively studied over the history of drag reduction investigations as it's easily available in a wide range of molecular weights with effective drag reduction concentrations. Investigations predominately are conducted in water, however, PEO has demonstrated drag-reducing properties in a wide range of solvents (Morgan, 1990).
Polyacrylamide (PAM) is another synthetic polymer widely commercially used as a drag-reducing constituent specifically within the hydraulic fracturing industry (Wever, 2011). This long chain flexible polymer is commonly synthesized in a variety of high molecular weights and is similar in structure to PEO except for an additional side-chain allowing the polymer to be less susceptible to shear degradation in high-velocity applications. The side chain of PAM provides a target for the functionalization of the monomer evolving variable behavior as a drag-reducing water-soluble agent. Functionalization, co-polymerization, and the process of polymerization of the acrylamide monomer with other monomer species influence whether the resulting polymer chain exists in a charged or natural state depending on the solution pH, and ionic strength.
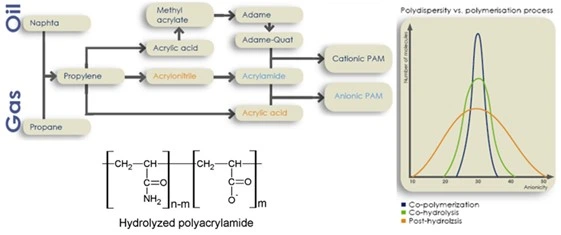
Partially hydrolyzed polyacrylamide (HPAM) is the most extensively used copolymer of acrylamide with a typical degree of hydrolysis ranging from 25%-35%. HPAM is produced either by the copolymerization of acrylamide with polyacrylic acid monomers in solution or by functionalization by hydrolysis of the acrylamide polymer post-polymerization. The ratio of monomer backbone units that exist in the hydrolyzed state to the total number of monomers within the polymer backbone defines the degree of hydrolysis. When acrylamide polymers undergo polymerization in the presence of a base in-situ hydrolysis occurs and produces HPAM in the range of 18 million molecular weight with predictable anionicity. When acrylamides are copolymerized in the presence of acrylic acid monomers the resulting polymer chain is anionic and in the molecular weight range of 20 million Daltons. Post-hydrolysis involves polymerizing acrylamide monomer then performing the hydrolysis with a base following polymerization producing 22 million Dalton HPAM polymers, with unpredictable anionicity and poor water solubility. The degree of anionicity and electrostatic charge within the polymer translates to a greater hydrodynamic radius in solution and as a consequence electrostatic repulsion improves the rheological properties increasing solution viscosity as compared to the uncharged equivalent. Commercial production of various PAM species from their raw materials is illustrated in Figure 2 alongside the molecular structure of HPAM (SNF US, 2012).
Figure 2: Top Left: Flow chart of common reagents used in the commercial production of synthetic drag reducing polymers. Right: Molecular weight and anionicity of the resulting products of various production techniques. Bottom left: Molecular structure of hydrolyzed polyacrylamide (SNF US, 2012).
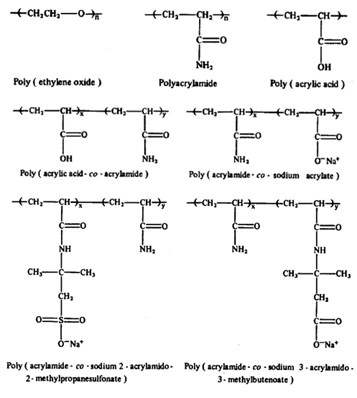
Dependent on the initial reactants, polymerization method, and reaction conditions result in polymers with diverse physical properties and compositions that have unique experimental drag-reducing behaviors. Many other monomer species and oligomers have been investigated in drag reduction studies and an expanded depiction of additional monomers used in commercial and scientific applications is shown in Figure 3; however, far more species have been studied and used commercially than contained in this list (Chai, 2019) (Stringfellow, 2014) (Sun, 2020). Due to the ease of production and accessibility PEO, PAM, and its derivatives have been the most common commercially used and scientifically investigated polymers. The wide variety of PAM co-polymers has allowed researchers to investigate the effects of the polymer-solvent interaction dependent on polymers molecular compositions to determine and understand the variables resulting in the most effective means of reducing turbulent drag in pipe flows.
Figure 3: Molecular structure of synthetic drag reducing polymers (Morgan, 1990).
Experimental Methods
To illustrate the benefit polymer additives provide to fluid flow it's important to first understand base solvent flow behavior. Experiments used to investigate drag reduction behavior commonly monitor a pressure difference observed between two fixed points of a smooth constant-diameter pipe while pumping fluid at a constant rate(Owolabi, 2017). The baseline measurement is taken with fresh water and then compared to a homogeneous polymer solution at a particular concentration. The drop in the pressure between the two fixed points allows for the calculation of the unitless friction factor. The friction factor (ƒ) is utilized to understand the pressure drop per unit length described by Equation 1.
Equation 1:
$$ f = {2 D \over \rho \overline{\mu}^2} \left({\Delta P \over L}\right)$$
Where D is the pipe inner diameter, ρ is the solution density, ū is the bulk flow velocity, and ∆P is the measured pressure drop over the fixed length L. Higher values for the friction factor translate higher friction loss within the given section. For friction reducers and their applications, lower friction factors are desired. Testing proceeds with gradually increasing the flow rate and monitoring the characteristic friction factor across various flow rates and regimes. The data is commonly presented on the log-log coordinates of friction factor vs Reynolds number. The ratio of the fluid's dynamic to viscous forces defines the Reynolds number and approximates the flow regime of a given system from laminar to turbulent. The Reynolds number is described by Equation 2.
Equation 2:
$$ R_e = {\rho \overline{\mu} D \over \eta}$$
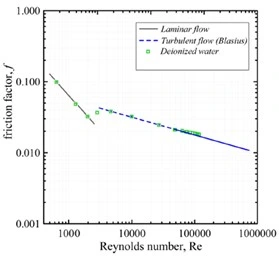
Where η is the solution viscosity. Data for the friction factor versus the Reynolds number for pure water across a wide range of flow velocities are presented in Figure 4 (Soares E. J., 2015). At low Reynolds numbers the fluid experiences laminar flow characterized by fluid layers moving smoothly through the pipe and past adjacent layers. In laminar flow adjacent fluid layers do not mix. In laminar flow, each fluid particle velocity independently follows the flow direction without turbulent tangential mixing and extends into Reynolds numbers of ~3000 described by Poiseuille's Law in Equation 3.
Equation 3:
$$ f = {64 \over R_e}$$
As the flow velocity continues to increase, turbulent eddies begin to develop in the flow path with intermittent puffs of turbulent slugs commonly referred to as transitional flow in the range of 2500<Re<4000. At higher Reynolds number the turbulent regime is apparent throughout the flow path and continues indefinitely as described by Blasius correlation in Equation 4 (Soares E. J., 2015) for water as the reference solvent. Though other solvents will have distinct characteristic slopes, all pure solvents undergo a laminar to turbulent transition as a function of increasing Reynolds numbers.
Equation 4:
$$ f = 0.314 R_e^{-0.25}$$
Because the friction factor has an inverse square relationship to the bulk flow velocity and the Reynolds number is only a single multiple of the bulk flow velocity the friction factor continually decreases as the flow velocity increases although the overall pressure loss within the system grows larger. It is important to understand the flow conditions when using the friction factor as a baseline for anticipated pressure losses since higher flow velocities inherently reduce the friction factor, but the overall pressure loss is much higher than that of raw pressure values at lower Reynolds numbers. This counter-intuitive reasoning is a product of how the friction factor and Reynolds number are calculated and how they relate to the physical interpretation of the values.
Figure 4: Friction factor behavior of deionized water as a function of Reynolds number demonstrating the transition from laminar to turbulent flow (Soares E. J., 2015).
When long-chain water-soluble polymers are introduced into the solution at a concentration as low as 5 ppm and the experiments are repeated the drag-reducing phenomena manifests as illustrated in Figure 5 (Soares E. J., 2019).
Figure 5: Friction factor behavior of polymeric solutions in water as a function of Reynolds Number demonstrating a reduction of the friction within the pipe flow as compared to that of the turbulent base solvent illustrated by the red line (Soares E. J., 2019).
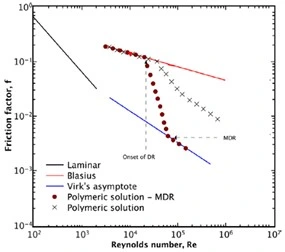
The presence of polymers in solution does not affect the friction coefficient in the laminar flow regime. Once the flow velocity exceeds the turbulent transition into full turbulence, a Reynolds number will be reached in which the friction factor of the solvent polymer pair reduces below that of the pure solvent. This point of divergence is known and the onset of drag reduction which continues to deviate from the base solvent behavior at higher flow rates. The variance between the friction factor of the polymer solution as compared to the base solvent is presented as the percentage of drag reduction achieved by Equation 5.
Equation 5:
$$ D R \% = {f_o - f_p \over f_o} * 100 $$
Where fo and fp are the friction factors of the base solvent and polymer solutions at the same Reynolds numbers respectively.
The trajectory of a specific polymer-solvent pair reduced below the base solvent trend with the response to an increase in the Reynolds number is unique and specific to the polymer-solvent pairs solution properties. Polymers that maximize the drag reduction potential of the solution at the lowest concentrations are most sought after for modern applications inclusive of hydraulic fracturing. The early work of Virk established a maximum asymptote of drag reduction which can be achieved but not exceeded by soluble polymers at which point solution properties can no longer improve the drag reduction potential (Virk, 1975). Virk's maximum drag reduction asymptote is described by the relationship in Equation 6 and presented by the blue line in Figure 5.
Equation 6:
$$ f = 2.63 R_e^{-0.58}$$
Due to the governing empirical equations of Blasius turbulent regime and the maximum drag asymptote, the maximum drag reduction percentage does not yield a specific value; but rather a maximum value specific to the Reynolds number approaching an asymptotic value. Table 1 illustrates the maximum achievable drag reduction percentage for aqueous solutions at a variety of Reynolds numbers. This is important in practice when comparing the efficacy of a variety of polymers where the polymer itself can influence fluid's Reynolds number with respect to the viscosity of the solution. When the addition of a polymer species doubles the solution's viscosity the Reynolds number is reduced in half resulting in a substantial decrease in the maximum drag reduction potential and potentially resulting in a Reynolds number lower than the critical value required to manifest the onset of drag reduction.
| Re | Blasius, ƒ | MDR, ƒ | DR % |
|---|---|---|---|
| 2,560 | 0.0444 | 0.0248 | 44% |
| 5,120 | 0.0373 | 0.0165 | 55% |
| 10,240 | 0.0314 | 0.0111 | 65% |
| 20,480 | 0.0264 | 0.0074 | 72% |
| 40,960 | 0.0222 | 0.0049 | 78% |
| 81,920 | 0.0186 | 0.0033 | 82% |
| 163,840 | 0.0157 | 0.0021 | 86% |
| 327,680 | 0.0132 | 0.0014 | 89% |
| 655,360 | 0.0111 | 0.0010 | 91% |
| 1,310,720 | 0.0093 | 0.0007 | 93% |
| 2,621,440 | 0.0078 | 0.0004 | 94% |
| 5,242,880 | 0.0066 | 0.0003 | 95% |
Prandtl-Karman Coordinates
Another traditional means of presenting data from drag reduction experiments in pipe flows charts the iterative relationship between \({1 \over \sqrt f}\) as a function of \(R_e \over \sqrt f\) known as Prandtl-Karman coordinates (Morgan, 1990). The two depictions of drag reduction character are used interchangeably throughout literature to describe the same phenomena. Prandtl-Karman coordinates system depicts increasing values of \({1 \over \sqrt f}\) as improved drag-reducing behavior as opposed to the prior ƒ versus Re coordinate plane where an inverse relationship is indicative of improved drag reduction. Here, the turbulent regime is defined by the Prandtl-Karman law. The governing equations for Prandtl-Karman coordinates for the laminar, Prandtl-Karman turbulent, and Virk's maximum drag reduction asymptote are respectively as follows:
Equation 7 - Laminar Flow:
$$ {1 \over \sqrt f} = {R_e \sqrt f \over 16}$$
Equation 8 - Turbulent Flow:
$$ {1 \over \sqrt f} = 4.0 \log_{10}(R_e \sqrt f)-0.04 $$
Equation 9 - Maximum Drag Reduction Asymptote:
$$ {1 \over \sqrt f} = 19.0 \log_{10}(R_e \sqrt f)-32.4$$
Figure 6: Prandtl-Karaman coordinates depicting drag reduction behavior of polymeric solutions as compared to the base solvent. Chart modified from (Morgan, 1990).
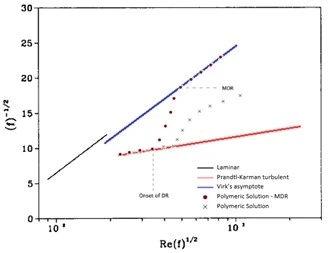
Though drag-reducing polymers follow similar experimental trends when charted and characterized, a wide variety of polymer compositions have been studied for their drag-reducing promise and compatibility for various environments, solvents, and applications.(Habibpour, 2017)(Al-Muntasheri, 2014)
Pipe Diameter
Figure 7 illustrates the effect of pipe diameter across identical concentrations of the same polymer solution as compared to the base solvent which, as expected, demonstrates flow behavior closely adhering to the Prandtl-Karman law for turbulent pipe flow (Virk, 1975). We find that as pipe diameter increases the onset of drag reduction increases to higher Reynold's values across the extension of pipe diameter from 2.92 mm to 32.1 mm with \(R_e \sqrt f\) values ranging from 400 to 4000 respectively.
Figure 7: Influence of pipe diameter on the onset of drag reduction in turbulent pipe flow (Virk, 1975).
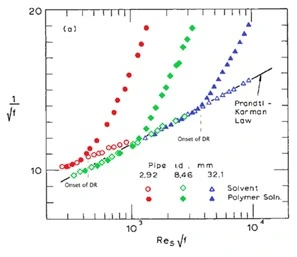
Upon further investigation of the flow character across the range of pipe diameters indicate the onset of drag reduction occurs once the fluid experiences a specific, well-defined critical wall shear stress denoted \(\tau_w^*\), in this instance \(\tau_w^* = 7 {N \over m^2}\) for all pipe diameters for a given polymer-solvent pair. The wall shear stress can be calculated by Equation 10 and is dependent on pipe diameter (D) and pressure loss per unit length and is proportional to the Reynolds number associated with the flow.
Equation 10 - Wall sheer stress:
$$ \tau_w = {D \over 4} \left({\Delta P \over L}\right)$$
This evidence suggests drag reduction occurs only after a specific wall shear stress is achieved independent of pipe diameter and only after the fluid transitions into the turbulent regime. This finding is of great practical significance when anticipating drag reduction at much larger scales concerning pipe diameter and flow velocity. In large diameter tubulars such as pipelines it should be understood whether the wall sheer stress exceeds this critical value prior to injecting any type of DRA as subcritical stress will not result in any pressure reduction or flow improvement.
Molecular Weight
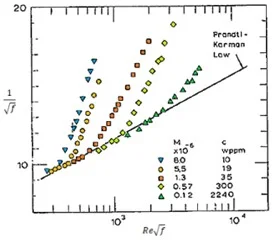
Further investigations illustrate as the polymer chain molecular weight increases, there is an earlier onset of drag reduction when comparing polymers differing only by molecular weight. Figure 8 demonstrates the onset characteristics of homogeneous PEO polymers of molecular weight ranging from 8*106 to 0.1*106 at variable concentrations in distilled water and constant pipe diameter (Virk, 1975). Although the higher molecular weight species were added at substantially lower concentrations than the lower molecular weight counterparts, it is clear the onset of drag reduction occurs at a lower value of \(R_e \sqrt f\) corresponding to the point the friction factor departs from that of the base solvent presented as the dark line adhering to the Prandtl-Karman law. These results indicate molecular weight is of great importance to reduce turbulent drag with improved efficiency. Higher molecular weight polymers require less concentration per unit volume to achieve a similar overall reduction of drag within a system. Supplementary investigations into the influence of molecular weight demonstrate that at sufficiently large molecular weight polymers can allow the solution to bypass the turbulent transition completely and reach the maximum drag reduction asymptote immediately after transitioning from the laminar regime.
Figure 8: Influence of molecular weight on the onset of drag reduction with PEO solutions (Virk, 1975).
Common analytical methods to quantify molecular weight look at light scattering measurements to determine the radius of gyration to describe and characterize dimensions of a polymer chain in solution. These measurements are closely associated with the number of monomers within a polymer species and thus approximate the polymer's overall molecular weight. Experiments investigating the influence of the polymer end-to-end chain length instead of molecular weight directly measured a single polymer species in two different quality solvents. Drag reduction measurements were taken for a homopolymer of identical molecular weight polymers at variable concentrations first in water, a good solvent, and then compared to a 0.6 M K2SO4 solution, a poor solvent. The polymer's radius of gyration in water was determined to be 95 nm and 65 nm in freshwater and 0.6 M K2SO4 solution respectively. The drag reduction experimental results are illustrated in the Prandtl-Karman coordinates of Figure 9 (Pruitt, Rosen, & Crawford, 1966).
Figure 9: Influence of solvent quality and concentration on the drag reduction capability of synthetic drag reducing polymers. Data from (Pruitt, Rosen, & Crawford, 1966).

Noteworthy findings from these experiments improve the understanding of polymer concentration and polymer coil size on the onset efficiency of a polymer-solvent pair as drag-reducing agents. Increasing the polymer concentration for both solvents demonstrate as concentration is increased from 10 to 250 ppm the onset of drag reduction is not influenced or altered; however, the angle of departure from the critical onset value \(R_e \sqrt {f*}\) with respect to the turbulent regime of the pure solvent increases in slope with increasing concentration of polymer in solution. The slope of departure of drag-reducing data from that of the solvent is defined as the slope increment (δ) and is an inherent property of a polymer-solvent pair and is greater than that of the base solvent when turbulent drag is reduced (Virk, 1975).
Comparison of the data between pure water and 0.6 M K2SO4 indicates that the critical value of \(R_e \sqrt {f*}\) increases as the quality of the solvent decreases with a critical \(R_e \sqrt {f*} = 500 \) for water and \(R_e \sqrt {f*} = 800 \) for K2SO4. Therefore, as the polymer's radius of gyration decreases in response to the presence of additional ions in solution, the solution is less effective as a drag-reducing formulation independent of polymer molecular weight. Building upon previous studies, not only will higher molecular weight polymers be more effective as a drag-reducing agent, but polymers with greater coil size in solution ultimately make more efficient drag-reducing agents by increasing the slope increment and decreasing the critical \(R_e \sqrt {f*}\). Most often anionic polymers are utilized in hydraulic fracturing due to electrostatic repulsion of the polymer chain promoting greater coil size in solution.
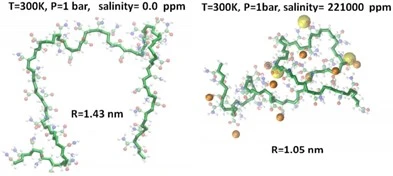
Molecular dynamic simulations of HPAM polymers help visualize the process of dissolved ionic species collapsing the polymeric chain in solution with the addition of ions (Abdel-Azeim, 2018). Figure 10 depicts the same HPAM polymer with a 50% degree of substitution under similar temperature and pressure conditions exposed to variable solution salinity alongside the measured radius of gyration (R). The yellow and brown spheres represent Ca2+ and Cl- respectively. The HPAM anionic character has an affinity for the solution cations which results in a collapse of the radius of gyration from 1.43 nm to 1.05nm limiting the degrees of freedom available to the polymer in solution rendering it a less effective drag reducing agent.
Figure 10: Influence of salinity on the molecular conformation and coil size of HPAM polymers in aqueous solutions. The yellow and brown spheres represent Ca2+ and Cl- respectively (Abdel-Azeim, 2018).
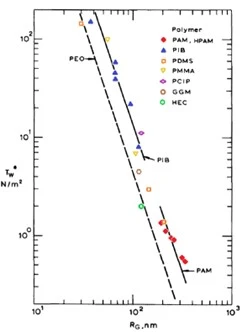
The correlation between the critical was shear stress, \(\tau_w^*\), at the onset of drag reduction and the measured polymer radius of gyration in for several polymers in water is presented in log-log coordinates of Figure 11 with an inverse correlation between the two properties. As Rg increases \(\tau_w^*\) deceases proportionally for a given polymer species (Virk, 1975). A polymer species unique relationship between Rg and \(\tau_w^*\) follow a narrow spread of values across a variety of polymers encompassing both organic and inorganic constituents. The data suggests \(\tau_w^*\) is approximately equal to the inverse of the Rg by a power of 2±1 as represented by the slope of the dark lines of Figure 11. The onset of drag reduction is a direct function of a polymer species' measured radius of gyration for a given polymer-solvent pair. This correlation, alongside prior experiments, establishes concentration is insignificant as it relates to the onset of drag reduction, but rather polymer coil size in solution is directly responsible for the phenomena to manifest.
Figure 11: Critical wall shear stress versus radius of gyration for a wide variety of drag-reducing water-soluble polymers.
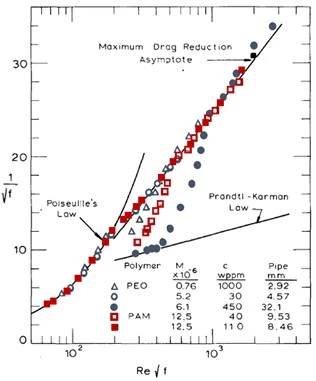
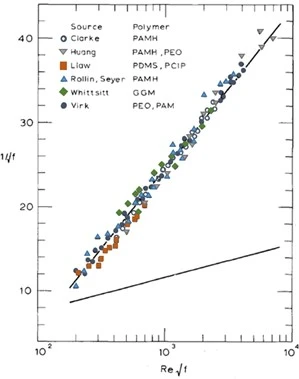
High Reynolds Behavior
Studies have demonstrated the onset of drag reduction and the slope increment can be influenced depending on the physical properties of the polymer-solvent pair. Increasing molecular weight, or random coil size in solution more specifically, can bring forward the onset of drag reduction at lower values of \(R_e \sqrt f \) after the flow bypasses the turbulent transition. Increasing the polymer concentration does not affect when onset occurs, but influences the slope increment particular to the polymer-solvent pair with an increased slope trajectory to the maximum drag reduction asymptote from that of the base solvent turbulent flow. Interestingly, despite a wide range of polymer-solvent interactions all effective drag-reducing agents ultimately reach the maximum drag reduction asymptote with nearly identical behavior at sufficiently high Reynolds values as depicted in Figure 12 (Virk, 1975). Across multiple polymer species, concentrations, molecular weights, pipe sizes, and undoubtedly a range of coil sizes and conformations, they all converge to the maximum drag reduction asymptote despite taking variable trajectories. This maximum drag reduction asymptote appears to be a universal feature of water-soluble polymers that continues to be observed across all investigations regardless of polymer-solvent interactions or oligomer composition and quantity. Additionally, these studies again demonstrate polymer solutions do not affect or reduce drag in the laminar flow regime but only mitigate frictional effects in the turbulent regime. This helps establish polymers are interacting with turbulent flow structures within the pipe itself as turbulence arises in response to increased flow velocities.
Figure 12: Demonstration of comparable drag reducing behavior at high Reynolds numbers across a wide variety of drag reducing polymer species (Virk, 1975).
Polymer Degredation
Prior investigations looked into modest Reynolds numbers to study and understand polymer behavior occurring near the laminar to turbulent transition providing insight to the critical Reynolds values where the onset of drag reduction occurs. Studies investigating polymer solutions exposed to higher shear environments for extended durations illustrate substantial degradation of the polymer and in turn degradation in drag reduction efficiency. Experiments which continuously pump and circulate a polymer solution through a pipe and continuously monitor the pressure difference between two fixed points illustrate a relationship of degradation of drag reduction over time. Data demonstrating the relationship between drag reduction percentage versus the amount of time a solution is exposed to a high shear environment is presented in Figure 13 (Soares E. J., 2015). Here the number of passes through the testing apparatus is used as a proxy to shear exposure time where one pass is equal to the flow rate divided by the total circulating volume. These results demonstrate as a polymer solution is continuously exposed to a high shear environment the drag reduction potential for the solution degrades incrementally over time and approaches an absolute drag reduction asymptote. This decrease in drag reduction potential is the result of the degradation of the long-chain polymers in solution interacting with turbulent forces within the pipe. We also note as the concentration of the polymer solution increases we do not circumvent polymer degradation, but higher concentration solutions ultimately approach a higher final value of drag reduction.
Figure 13: Degradation of drag reduction percentage for PAM versus the number of passes through a testing apparatus at a constant flow rate (Soares E. J., 2015).
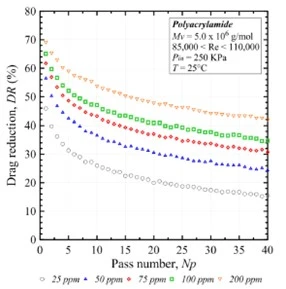
The relative loss of drag reduction between different concentrations of a given polymer species shows higher concentrations of polymers maintain a higher relative drag reduction when compared to their initial state. Figure 14 shows data of relative drag reduction as a function of time where the 200 ppm concentration retains 70% of its initial drag reduction whereas lower concentrations retain only 30% of its drag reduction potential after sequential passes. To mitigate the loss of friction reduction of polymer solutions exposed to high shear environments over extended periods higher concentrations are needed to maintain drag reduction efficiency.
Figure 14: Relative drag reduction of PAM versus the number of passes through the testing apparatus at a constant flow rate (Soares E. J., 2015).

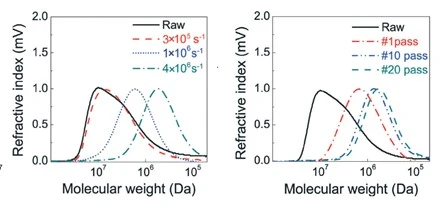
Similar work reveals drag reduction is significantly reduced over time to variable extents in high shear environments for nearly all types of polymers regardless of molecular composition at sufficiently high flow rates. Experiments confirm degradation is the direct result of destruction and chain-scission of the polymer chain is shown in Figure 15 by pumping a PAM solution through a tight capillary inducing a sudden exposure to extremely high shear rates ranging between 3x105s-1 and 4x106s-1 (Xiong, Purswani, & Pawlik, 2020). The graph of the right presents the refractive index recorded from size exclusion chromatography to determine the molecular weight of the polymer solution after a single pass through three different high shear environments. At 3x105s-1 shear rate, little degradation of the polymer molecular weight is measured indicating a lower bound exists where the polymer chain will not degrade and the turbulent energy is not sufficient enough to cause mechanical chain rupture at low enough flow velocities. At higher shear rates we see that a significant reduction of molecular weight occurring within the polymer solution and a much more normal distribution of molecular weight results as compared to the sample's original molecular weight distribution. The chart on the right reveals the resulting molecular weight distribution of a PAM solution after being exposed to a 1x106s-1 shear environment multiple times with measurements taken after 1, 10, and 20 passes of the PAM solution through a high shear environment. As the solution is passed through the high shear environment we see the molecular weight decrease and ultimately arrive at a stable molecular weight equilibrium after 20 passes. The equilibrium value of molecular weight agrees perfectly with the prior drag reduction degradation reaching an asymptotic value.
Figure 14: Degradation of molecular weight of PAM when exposed to high shear regimes. Left: Molecular weight distribution of a PAM solution after a single pass through a range of shear rates. Right: Resulting molecular weight distribution after multiple passes of a PAM solution through a 1x106s-1 shear environment (Xiong, Purswani, & Pawlik, 2020).
Conclusion
When long-chain polymers are introduced into aqueous solutions they provide a substantial amount of friction reduction as compared to the base solvent alone. This phenomenon has been studied over a broad range of polymer species, compositions, and flow environments over the past several decades. The practical applications of drag-reducing polymers extend across multiple industries, and one of the largest and most common commercial use of drag-reducing polymers is within the hydraulic fracturing industry since they provide an economically attractive means of reducing the pump and pressure requirements necessary to break down rock formations deep in the subsurface under miles of wellbore piping. Each polymer species has unique friction reduction behaviors and the efficiency of a polymer species to reduce drag in solution is a function of the chemical composition and the physical properties of the polymer chain. For a given polymer species the onset of drag reduction occurs at a critical shear rate independent of pipe diameter. This allows for the scalability of laboratory results to predict anticipated pressures in commercial fracturing applications. For hydraulic fracturing applications to benefit from drag reduction sufficiently high pumping rates must be obtained. Common fracturing operations occur in pipes of internal diameters ranging from 4"-5.25" at a rate greater than 60 barrels per minute which equates to a wall shear stress in the range of \(\tau_w \approx 100 - 1000 \left( N \over m^2 \right)\). This anticipated wall shear stress is far beyond the critical wall shear stress evaluated for polymer solutions in this work. Polymer selection for fracturing operations should not rely on the drag reduction onset criteria since the flow velocities common to the operation are well into the turbulent regime with sufficiently high Reynolds values where drag reduction onset is certain to occur. As the molecular weight of the polymer increases, drag reduction onset occurs at a lower Reynolds value. Similar to pipe diameter, the onset of drag reduction is not an important variable to consider in hydraulic fracturing being that sufficiently high flow rates are achieved where the early-onset distinction between polymer species would render itself a reasonable selection criterion. However, higher molecular weight polymers are certainly more favorable as a drag-reducing agents as they require substantially less volume to produce maximum drag reduction in solution providing the most economically attractive option. Alongside molecular weight, the base fluid water quality should contain a little TDS as possible to create the largest polymer coil volume in solution. The presence of ionic species in solution collapse the free coil size of drag-reducing polymers which can negate the advantages higher molecular weight polymers provide. At sufficiently high Reynolds values multiple polymer species demonstrate the ability to achieve maximum drag reduction independent of the polymer composition, concentration, or pipe diameter and collectively adhere to the maximum drag reduction asymptote. The most important, and often overlooked property of drag-reducing polymers within hydraulic fracturing is their susceptibility to degradation once exposed to high rate flow conditions for an extended period as is common within fracturing treatments. For a given polymer species the relative loss of drag reduction capability over time can be combated by over 30% simply by increasing the polymer concentration in solution. The best possible performance outcomes for drag-reducing agents utilized during hydraulic fracturing operations is a high molecular weight polymer applied in high concentrations to combat degradation of the extremely high shear environments associated with fracturing operations.
References
1. Abdel-Azeim, S. a. (2018). Dynamics, aggregation, and interfacial properties of the partially hydrolyzed polyacrylamide polymer for enhanced oil recovery applications: insights from molecular dynamics simulations. Energy & Fuels, 3335-3343.
2. Al-Muntasheri, G. A. (2014, April 17). A Critical Review of Hydraulic Fracturing Fluids over the Last Decade. Society of Petroleum Engineers, 10.2118/169552-M.
3. Burger, E., Munk, W., & Wahl, H. (1982). Flow increase in the Trans Alaska Pipeline through the use of polymeric drag reducing additive. Journal of Petroleum Technology, 337-386.
4. Chai, Y. e. (2019). Mechanistic study of drag reduction in turbulent pipeline flow over anionic polymer and surfactant mixtures. Colloid and Polymer Science, 1025-1035.
5. Habibpour, M. a. (2017). Drag reduction behavior of hydrolyzed polyacrylamide/xanthan gum mixed polymer solutions. Petroleum Science , 412-423.
6. Morgan, S. E. (1990). Water-soluble polymers in enhanced oil recovery. Progress in polymer science, 103-145.
7. Owolabi, B. E. (2017). Turbulent drag reduction by polymer additives in parallel-shear flows. Journal of Fluid Mechanics, 827.
8. Pardo, D., & Torres-Verdin, C. (2012). Hydrofracture Diagnosis in Open-Hole and Steel-Cased Wells Using Borehole Resistivity Measurements. Society of Exploration Geophysicists.
9. Pruitt, G., Rosen, B., & Crawford, H. R. (1966). Effect of Polymer Coiling on Drag Reduction. Dallas, TX: Westen Co.
10. SNF US. (2012, September). SNF Polymers and their Chemistry. Retrieved from https://www.snf.us/wp-content/uploads/2014/08/EOR-Oil-30-Years-of-EOR.pdf
11. Soares, E. J. (2015). Loss of efficiency of polymeric drag reducers induced by high Reynolds number flows in tubes with imposed pressure. Physics of Fluids, 125105.
12. Soares, E. J. (2019). Review of mechanical degradation and de-aggregation of drag reducing polymers in turbulent flows. Journal of Non-Newtonian Fluid Mechanics , 104-225.
13. Stringfellow, W. T. (2014). Physical, chemical, and biological characteristics of compounds used in hydraulic fracturing. Journal of hazardous materials, 37-54.
14. Sun, D. e. (2020). Adsorption behavior and shear degradation of ultrahigh‐molecular‐weight hydrolyzed polyacrylamide in a capillary flow. Journal of Applied Polymer Science, 470-482.
15. Toms, B. A. (1948). Some observations on the flow of linear polymer solutions through straight tubes at large Reynolds numbers. Proc. of In. Cong. On Rheology, 135.
16. Virk, P. S. (1975). Drag reduction fundamentals. AIChE Journal, 625-665.
17. Wever, D. A. (2011). Polymers for enhanced oil recovery: a paradigm for structure-property relationship in aqueous solution. Progress in Polymer Science, 1558-1628.
18. Xiong, B., Purswani,
P., & Pawlik, T. (2020). Mechanical degredation of polyacrylamide at ultra
high deformation rates during hydraulic fracturing. Environmental Science,